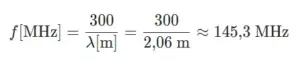Frequenz
Die Wechselspannung in unserem Stromnetz schwingt 50 mal in der Sekunde hin und wieder zurück. Die Anzahl der Schwingungen pro Sekunde nennt man Frequenz. Die Frequenz wird in der Einheit Hertz mit der Abkürzung Hz angegeben. Ein Hz entspricht genau einer Schwingung pro Sekunde. Das Stromnetz hat also eine Frequenz von 50 Hz.
Im Funk benutzen wir auch elektrische Schwingungen, allerdings mit sehr viel höheren Frequenzen als das Stromnetz, z. B. 144000000 Hz. Bei so vielen Ziffern wird es schnell unübersichtlich. Daher verwenden wir den Ausdruck Megahertz (MHz) für eine Million Hertz und sagen „144 Megahertz“. Wir haben das Einheitenvorzeichen „M“ verwendet und es vor die eigentliche Einheit „Hz“ gesetzt. Damit drücken wir aus, dass der angegebene Wert mit einer Million multipliziert wird.
Sinusschwingung
Elektrische Schwingungen bestehen aus Wechselspannung, die abwechselnd positive und negative Polarität annimmt. Die Spannung wechselt meist aber nicht abrupt von positiv nach negativ und zurück.
Wie man im Bild sehen kann, schwingt die Spannung im Stromnetz beispielsweise immer wieder sanft wie ein Pendel von Plus über 0 nach Minus und wieder über 0 zurück nach Plus.

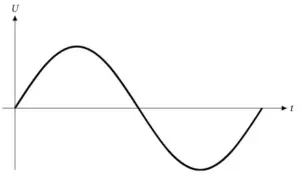
Diese Grundform nennt man Sinusschwingung. Man kann sie gut an ihrem wellenförmigen Verlauf erkennen. Neben den sinusförmigen Wechselspannungen gibt es eine Vielzahl weiterer Schwingungen. Die bekanntesten sind folgende:
Rechteckförmige Schwingung
Dreieckförmige Schwingung
Sägezahnförmige Schwingung
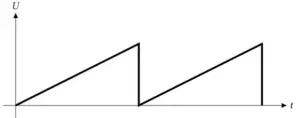
Amplitude und Periode
Den maximalen Abstand von der Nulllinie bis zum höchsten oder tiefsten Punkt der Wechselspannung nennt man wie in Abbildung dargestellt Amplitude.
Eine Sinusschwingung besteht aus einer positiven und einer negativen Halbwelle. Dafür benötigt die Sinusschwingung eine gewisse Zeit (tt). Die Zeitspanne vom Beginn einer positiven Halbwelle bis zum Ende der darauffolgenden negativen Halbwelle nennt man Periode oder auch Periodendauer. Nach Ablauf einer Periode beginnt der Vorgang von Neuem.

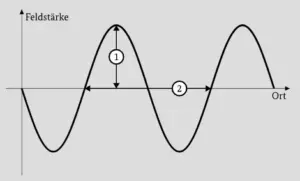
Funkwellen
Leitet man eine elektrische Schwingung an eine Antenne, dann strahlt diese eine Funkwelle ab. Funkwellen gehören genauso wie das Licht zu den elektromagnetischen Wellen und breiten sich daher mit Lichtgeschwindigkeit aus. Diese beträgt – im sogenannten Freiraum, wo es keine Hindernisse gibt – annähernd 300000 Kilometer pro Sekunde.
Funkwellen bestehen aus Wellenbergen und Wellentälern. Je höher die Wellenberge und je tiefer die Wellentäler sind, umso stärker ist das Funksignal. Man spricht in diesem Zusammenhang von der Feldstärke. Die Höhe eines Wellenberges bzw. die Tiefe eines Wellentals nennt man wie bei der elektrischen Schwingung auch hier Amplitude.
Wellenlänge
Den Abstand zwischen zwei Wellenbergen bzw. zwei Wellentälern nennt man Wellenlänge. Die Wellenlänge ist abhängig von der Frequenz. Je größer die Frequenz, desto kleiner die Wellenlänge. Die Wellenlänge wird mit dem griechischen Buchstaben λλ (Lambda) bezeichnet und üblicherweise in Meter (m) angegeben.
Der Zusammenhang zwischen der Frequenz und der Wellenlänge ergibt sich aus der Lichtgeschwindigkeit von 300000 km/s. Eine Welle mit einer Frequenz von 1 Hz breitet sich 300000 km aus, bevor auf einen Wellenberg ein weiterer Wellenberg folgt. Eine Welle mit einer Frequenz von 1000 Hz breitet sich nur 300 km aus, bevor auf einen Wellenberg wieder ein Wellenberg folgt. Bei 1000000 Hz also 1 MHz sind es nur noch 300 m.
Daraus ergeben sich folgende Formeln, mit denen sich leicht zwischen Frequenz ff (in MHz) und Wellenlänge λλ (in Metern) umrechnen lässt:
Die beiden Formeln finden sich auch in der Formelsammlung, die bei der Prüfung als Hilfsmittel vorliegt.
Teilt man also 300 durch die Wellenlänge in Metern, erhält man die Frequenz in MHz. Und genauso andersherum: Teilt man 300 durch die Frequenz in MHz, erhält man die Wellenlänge in Metern.
Wollen wir also beispielsweise die Wellenlänge der Frequenz 145,3 MHz berechnen, dann setzen wir diese in die erste Formel ein und lösen dann:

Genauso funktioniert es andersherum. Setzen wir die Wellenlänge von 2,06 m in die zweite Formel ein, dann kommt die ursprüngliche Frequenz heraus:
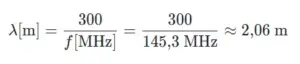
Die gerundete Wellenlänge wird übrigens häufig verwendet, wenn man über Frequenzbereiche spricht. Man spricht dann von einem Frequenzband oder kurz Band, z. B. dem 2 m-Band.